ttonon
Members-
Posts
359 -
Joined
-
Last visited
Everything posted by ttonon
-
Mystery of misbehaving F3 note.
ttonon replied to Łukasz Martynowicz's topic in Instrument Construction & Repair
Lukasz, from my calculations, I see no possible resonance interference with the tongue vibration. This applies to both Helmholtz and quarter-wave tube resonance. I thus cannot make a suggestion here, only I'm still not clear on what the basic problem is. Are you saying that all the F3 reeds you put into the "bad" cavity show the same problem? Also, that when you put those same reeds into a different cavity but with the same dimensions of the "bad" cavity, there is no problem? Best regards, Tom -
Mystery of misbehaving F3 note.
ttonon replied to Łukasz Martynowicz's topic in Instrument Construction & Repair
Hi Lukasz, I just now heard your wav file and I agree, the 1st and 3rd sounds seem restricted, and the 2nd and 4th more open or free. In my experience, such a restricted sound occurs when the mounting of the reed - most often the geometry of the cavity - begins to acoustically interfere with tongue vibration. For instance, if the port is too small, or even if the leather valve isn't opening completely enough. Alternatively, there could be some defect in the construction of the reed, such as a burr, or other way to interfere with tongue vibration. Your guess that the problem lies in a restricted second partial seems to be borne out by the spectrum. In the bad note, that partial is about 13 dB below the fundamental, and in the good note, it's only about 5 dB below the fundamental. I'm not sure there's evidence in the spectrum for your claim that the energy of that second partial is fed into the higher partials, which from my experience would be an odd occurrence, knowing what I know about the conversion of pressure pulses to audible sound. We can notice that the bad note has also a greatly reduced 8th partial, compared to that of the good note, but I doubt that has anything to do with what we hear, since the pitch of that partial is about 22,000 Hz, far above our normal hearing range. However, your discovery of this reduced second partial may give us a clue. If you'd go through the trouble of presenting here all the exact 3-D dimensions of the cavity and the size of the port, I'd be glad to take a look at it, possibly finding an identification of the second partial frequency with some way the cavity could resonate. If it's a simple rectangular cavity, it should be easy to do. Best regards, Tom -
Mystery of misbehaving F3 note.
ttonon replied to Łukasz Martynowicz's topic in Instrument Construction & Repair
Hi Lukasz, Audacity enables the calculation of a frequency spectrum showing a rectilinear graph, with sound intensity on the vertical axis and frequency on the horizontal axis. I believe that such a representation is much more useful than the kind of spectrum you posted here. If you can't figure out how to get that graph on Audacity, let me know and I can perhaps lead you through it. More basically, I don't know what your "problem" is. Apparently there's a problem with the sound of two different F3 reeds when alternatively mounted in the same cavity. Is this correct? If so, could you please explain in detail the problem in the sound? Do you think you see the "problem" in the spectrum you posted? If so, please explain. In the "Bellows pressure and musical pitch" thread, if I recall, you thought that the poor sound was because of a pronounced harmonic and I suggested you do a spectrum analysis. Do you still think the problem is with a pronounced harmonic? If so, the kind of spectral graph I describe will be most useful. Regards, Tom Tonon www.bluesbox.biz -
Concertina in an Extreme Environment
ttonon replied to Fifer1mr's topic in Instrument Construction & Repair
Fifer, I'm intrigued by your planned journey, and if appropriate, could you please explain some things about the mission? It's main strokes, purpose, and the organizations behind it? Are there chiefly scientific goals? Methinks it's a great opportunity for experiences that you will never forget. Best regards, Tom -
Concertina in an Extreme Environment
ttonon replied to Fifer1mr's topic in Instrument Construction & Repair
Hi Fifer, You'd want to be aware that the reeds might buzz when you try to play the instrument when it hasn't warmed up all the way to room temperature after a cold transport outdoors. That's because the vibrating tongues might rub against the end walls of their slots. The different coefficients of linear thermal expansion (CTE) in the reed plate material and the tongue material will cause the tongues to close the small air gap between them when at the lower temperatures. The extent of this rubbing will be affected by the kind of material used in the reed construction. The CTE for brass is about 10E-6 per degree F; for Aluminum, about 12.5E-6, and for steel about 6.5E-6. It's the difference between these values that matters. Thus for steel tongues in brass plates, the difference is 6E-6 and for aluminum plates with steel tongues it's 3.5E-6. Let's say the outside temperature is - 40 F, and let's consider one of the longer reeds, with tongues about 2 inches long. The reeds were designed (gaps were set) for room temperature, say 70 F. The delta T to consider is thus 40 + 70 = 110 F, so multiplying the delta CTE's, the delta T's, and the nominal lengths, we calculate the difference between how much the tongue lengths expand/contract and how much the slot openings expand/contract, as about 0.00076 inch for the brass/steel combination and about 0.0012 for the aluminum/steel combination. I believe I recall Dana saying that his gaps are roughly a half thousands, or 0.0005 inch, on average. We can thus conclude that for some concertina reeds, and for the lowest temperatures, there will be closure of gaps. This is especially true considering expected variations in workmanship, and for the tight condition at the corners of the slot/tongue gaps. In fact, I've noticed that with my Baldoni accordion with handmade reeds, I'd get buzzing when I brought it inside from winter temperatures only as low as about freezing. I would often press on the keyboard and gently draw air in and out of the box, until its interior warmed. I concluded that the variation in workmanship plays a large role here. Best regards, Tom www.bluesbox.biz -
Bellows pressure and musical pitch
ttonon replied to ttonon's topic in Instrument Construction & Repair
Lukasz, I recall some of those discussions, and my conclusions are that - as a video showed - there needs to be minute tongue vibration while in its standoff position. The only physical mechanism I can think of for that vibration is the same one observed in many other systems. It's called, "vortex induced vibration." With it, vortices are shed periodically, forming "von Karman vortex streets" downstream. This shedding causes air pressure oscillations that excite the vibrator, and they couple with the vibrator, forming at a frequency close to the natural vibration frequency of the tongue. Eventually, the amplitude of tongue vibration becomes large enough to allow the tongue to enter the slot. Once that happens, the normal self-excitation mechanism takes over and the tongue vibration amplitude rapidly builds up to its normal level. I say "rapidly" only in a relative sense, since compared to other sound sources, the start transient for free reeds is rather long. Best regards, Tom- 31 replies
-
Bellows pressure and musical pitch
ttonon replied to ttonon's topic in Instrument Construction & Repair
Hi Dana, Perhaps we need to coin a different word for when those high frequency reeds fail to start because of a resonance conflict with the air of the cavity. Let me propose something like "dead," but I'm not too creative at the moment and maybe someone else has a better term. Of course there could be difficulty in distinguishing whether that reed is really dead or if it fails to start for other reasons, such as for instance, too small a quiescent standoff distance. I agree that the 15th harmonic is virtually always negligible and it's highly unlikely that a hindrance to its expression would prevent tongue vibration. I think at the time I illustrated the magnitudes only to give the reader a better idea of the scope and relative comparisons of the ideas I was trying to communicate. But how about for the second partial? As you well know, a chamber has many characteristics, and many involve specific dimensions, as you observe with the brightness effect of cavity height. The Helmholtz conflict I describe is only one, and being a universal property, it involves only the volume and port of the cavity. Another is the quarter wave tube vibration that is treated in the columns on the right in the Table. I don't know how much clearer I can be. I'm pointing out a simple way in which two resonant systems - the tongue and the air in a resonator - can interfere. I have not proved it rigorously, but I think that the known observation that a dead reed with a particular cavity can be brought to life through a minor tweak to a (any?) cavity dimension or a drilled hole, strongly points to resonance conflict, particularly since calculation proves that the Helmholtz frequencies coincide with the fundamental pitch of the tone in those cases. There certainly are electrical circuit analogies, and all that adds a broad base of evidence for my suggestion. Let me try this. With a standard Helmholtz geometry, during resonance, air pulses in and out of the aperture and pressure in the cavity oscillates. If you put a hole in the wall of the cavity, small compared to the aperture opening, you'd sense air pushing in and out because it's driven by those pressure oscillations. This airflow is what the Helmholtz resonator wants to do. Put a reed in the wall of the cavity and stop it from vibrating, say by gluing it's tip to the plate. During Helmholtz resonance, you would probably sense air fluctuating in and out through the minute leakage gaps between tongue and slot wall. Now release the tongue, and you can reason that the Helmholtz resonator will want to impart vibration in the tongue. But the tongue has it's own way of exciting it's own motion (not explained here), and why assume that what the resonator wants to do is the same kind of airflow the tongue needs to vibrate? You can reason by considering the phase relationship between cavity pressure oscillation and the oscillating flows through both the aperture and the reed. Each system demands its own phase relation between displacement and pressure oscillation. Why should they be the same? That's why I'm suggesting that there's a conflict. Before I looked into this, I naively thought - as many others did - that perhaps Helmholtz resonance can be exploited in helping and amplifying tongue vibration, by designing tuned cavities for each reed. But when I did the experiments, I found the opposite. Coincidence with Helmholtz or quarter wave tube resonance killed the reed! That's when it seemed obvious to me that Helmholtz resonance may indeed be a key reason for "dead" reeds. Best regards, Tom- 31 replies
-
- 1
-

-
Bellows pressure and musical pitch
ttonon replied to ttonon's topic in Instrument Construction & Repair
Auldfellowmelad, thanks for your suggestions and encouragement. I can find no record in the scientific literature that deals with the physics of tongue vibration in the free reed. There are articles on more general topics, and several very good articles on the acoustic sound field produced by the reed. But the latter regard the reed vibration itself only as an input sinusoidal vibrating valve. They don't "solve" for the tongue vibration on its own. Thus if any reed manufacturer in Italy made such attempts, it's largely buried to the public. From my own experience though, I doubt it. The accordion/reed industry in Italy and probably elsewhere is dominated by fixed ideas that were developed over a hundred years ago, and the field is populated by closed minds. Many people in this industry didn't think it possible that my acoustic technology for pitch bending in the free reed was even possible, and some claimed that they already knew all about it. Humorous, to say the least. Your recommendation to visit a maker is a very good one. I should mention that Dana and I have had extensive discussions via email, which probably took us to the extent of our communicable knowledge on the subject. In addition, Dana has provided me with a couple expertly-made reeds to my specifications and with which I plan to use in my own experimentation. More future plans that I hope to accomplish. Best regards, Tom- 31 replies
-
Bellows pressure and musical pitch
ttonon replied to ttonon's topic in Instrument Construction & Repair
Hi Lukasz, it's not clear. You say you measured the spectrum when the reed speaks on your table. Did you also measure the spectrum when it's speaking in the instrument? Regards, Tom- 31 replies
-
Bellows pressure and musical pitch
ttonon replied to ttonon's topic in Instrument Construction & Repair
Ales, yes, two completely different phenomenon, involving different physics, with vastly different remedies. Thanks for pointing it out. Regards, Tom- 31 replies
-
- 1
-

-
Bellows pressure and musical pitch
ttonon replied to ttonon's topic in Instrument Construction & Repair
Lukasz, you take me from "beating" to "buzzing," and I don't understand either. But your claim that a higher partial is overly emphasized intrigues me because such an event is rare, in my experience. Sometimes with free reeds the second partial (one above the fundamental) can have a little greater amplitude than the fundamental, but I don't know if it's really noticeable by ear. I suggest you first verify that what you say is true, and that's easy to do. Make a digital recording of the tone with an audio recorder and feed the data in a spectrum analyzer, such as Audacity, free software available on the web. You can then see very clearly whether there's a partial with an abnormally high amplitude. If that's the case, we'd know the frequency of that partial and that could be a clue in determining what cavity dimension is involved, if any. I may be wrong but I think you totally misunderstand the purpose of the table I presented. I'm not trying to design reed cavities using Helmholtz theory. I'm suggesting that the choking we observe, especially with the higher frequencies, is when the air resonance in the cavity matches close enough the fundamental of the musical tone. Air resonance happens in most all musical instruments, although the free reed is exceptional in that it occurs only sporadically, without a well understood benefit to the musical tone. I also suggest that a match with one of the lower partials can also cause problems. Once you understand the self-excited vibration of the tongue you will see the sense to this suggestion. For a builder like you, there's no need to even think about this or do any calculations. If you experience reed choking, all you do is try one of your trusted remedies and it will work, whether or not you understand why. Being human, you come up with your own theory on why, without any need to compare it with established acoustical principles. For me, there's value in identifying the underlying physics, but you don't really care about that and there's no reason you need to care. I offer this information only for those curious enough in this way. Best regards, Tom- 31 replies
-
- 1
-

-
Bellows pressure and musical pitch
ttonon replied to ttonon's topic in Instrument Construction & Repair
Auldfellowmelad, I think I made my aim clear. I'm intending to understand the physics behind the tongue vibration in the free reed. As far as I know, no one has done this before. It's a challenge, and it brings me great pleasure in going about the process. I hope I succeed to some degree, at least to be able to publish it for the world to see. Is that enough?- 31 replies
-
Bellows pressure and musical pitch
ttonon replied to ttonon's topic in Instrument Construction & Repair
Lukasz, you confuse me greatly. Why do you assume that the Helmholtz model requires orthogonal cavities? The Helmholtz model assumes that all acoustic wavelengths are much larger than any of the resonator dimensions. This allows us to treat the three separate components, Volume, Aperture Area, and Aperture (effective) Length as parts of a "lumped parameter" system. That means the shape of the volume doesn't matter. Spherical, cubical, rectangular, cylindrical, etc. doesn't matter. Only the Volume of the cavity matters. I mention "orthogonal" in my article only to make the volume calculation simple. Thus you're assumption that my model for choking reeds requires orthogonal cavities is erroneous. Concerning your F3 reed problem, what do you mean by "beating?" In acoustic terminology, beating usually refers to the interference of two sounds that are separated by small frequency differences. What is that one F3 reed beating against? It's also difficult for me to visualize the construction, and maybe a picture would help. I have some ideas, but I want to be sure I'm understanding the issue. Best regards Tom- 31 replies
-
Bellows pressure and musical pitch
ttonon replied to ttonon's topic in Instrument Construction & Repair
Hi Alex, my guess is that the valve enables a larger body of air to vibrate with the tongue, thus causing a higher inertial load to the vibration. It "cups" the tongue with a larger air mass, forcing more air to participate in the vibration. In addition it adds its own mass to the vibration. With any single parameter spring-mass vibration, larger mass results in lower natural frequency. One reason for the absence of leather valves on the high pitched reeds is to lessen the tendency to choke. At least with accordions, when two tongues share the same cavity, the lack of a leather on the one reed provides air leakage as the other speaks. This leakage lessens the effect of the Helmholtz vibration on the speaking reed. For my work, I sometimes need valves on all reeds and when I installed valves for the highest reeds, they tended to choke. As I mention in my PICA article, a similar solution is to drill a small hole through the cavity wall or the reed plate. Thus, the air vibration caused by Helmholtz is not concentrated solely on the playing reed. In other words, leakage through the hole lessens the acoustic coupling to the cavity. Incidentally, this is another phenomenon that you cannot explain with Lukasz's "length theory." Best regards, Tom- 31 replies
-
Bellows pressure and musical pitch
ttonon replied to ttonon's topic in Instrument Construction & Repair
Lukasz, thanks for your comments, which indicate a considerable amount of experience in trying to understand the idiosyncrasies of the free reed, which I believe is among the most complicated sources for musical tone. I think I can explain the observation you mention in your above quote by means of the following table, which is in the PICA article I mentioned above. (If you can't take the horse to water, bring the water to the horse 😋) - - - - - - - - - - - - - - Table 1: Cavity Geometry from Resonant Acoustic Model Calculations -------- Helmholtz Calculation ------- --- Tube Calculations --- Note Partial ν λ Vadj W L d t H S max H fixed L-QW L-FW G1 1 49 277 -0.26 1.00 3.00 0.40 0.25 166 41.5 0.8 68.69 138.12 G1 9 441 30.7 -0.26 1.10 3.00 0.32 0.38 1.11 4.61 0.8 7.12 15.09 G1 11 539 25.2 -0.26 1.20 3.50 0.40 0.38 0.84 3.77 0.8 5.67 12.27 G1 15 735 18.4 -0.26 1.20 3.50 0.40 0.38 0.48 2.77 0.8 4.00 8.92 G2 1 98 138 -0.19 1.00 2.50 0.40 0.25 49.9 20.8 0.75 34.10 68.94 G2 6 588 23.1 -0.19 1.10 2.50 0.32 0.31 0.85 3.46 0.75 5.26 11.28 G2 7 686 19.8 -0.19 1.20 2.70 0.32 0.30 0.56 2.97 0.75 4.45 9.64 G3 1 196 69.2 -0.19 1.00 2.00 0.30 0.25 10.1 10.4 0.50 16.87 34.38 G3 4 784 17.3 -0.19 1.10 2.00 0.32 0.30 0.65 2.59 0.50 3.83 8.40 G3 5 980 13.8 -0.19 1.20 2.70 0.40 0.30 0.41 2.08 0.50 2.92 6.65 G4 1 392 34.6 -0.13 1.00 1.80 0.30 0.25 2.84 5.19 0.50 8.22 17.08 G4 3 1176 11.5 -0.13 1.10 1.80 0.30 0.25 0.34 1.73 0.50 2.45 5.55 G4 4 1568 8.65 -0.13 1.20 1.80 0.32 0.20 0.24 1.30 0.50 1.77 4.13 C5 1 523 25.9 -0.12 1.00 1.70 0.30 0.25 1.72 3.89 0.38 6.05 12.75 C5 3 1569 8.64 -0.12 1.10 1.70 0.32 0.20 0.27 1.30 0.38 1.77 4.13 C6 1 1046 13.0 -0.07 1.00 1.50 0.32 0.20 0.63 1.94 0.20 2.85 6.29 C6 2 2092 6.48 -0.07 1.00 1.50 0.32 0.20 0.19 0.97 0.20 1.23 3.04 C7 1 2093 6.48 -0.08 1.00 1.25 0.32 0.18 0.24 0.97 0.15 1.25 3.05 C8 1 4186 3.24 -0.02 0.80 1.00 0.32 0.13 0.11 0.49 0.15 0.49 1.46 Notes: All lengths in inches Note is nomenclature for piano keyboard, typically found in concertinas Partial is partial number ν is frequency of corresponding partial (Hz) λ is wavelength of corresponding partial Vadj is volume adjustment to orthogonal cavity structure, to account for reed volume (cubic inches) W is orthogonal cavity width in Helmholtz model L is orthogonal cavity length in Helmholtz model d is aperture diameter t is aperture length (Action Board thickness) H is calculated orthogonal cavity height for Helmholtz resonance, Equation 2 & 3, k = 0.6 S max = 0.15λ is about maximum size of any component for Helmholtz model to remain accurate H fixed is cavity height used for tube calculations in next two columns L-QW is length of cavity for quarter-wave model, Equations 4 & 5, k = 0.6 L/2-FW is length of cavity for partitioned full-wave model, Equations 6 & 7, k = 0.6 BOLD numbers indicate regions on the musical scale where resonance occurs and/or where reed choking may occur (when Partial = 1) - - - - - - - - - - - - - - - The notes after the table should be adequate explanation. For the calculations in this table, I assumed what I think are typical cavity dimensions (L, W, H). The bold numbers indicate the cavity dimensions that form resonant geometries with the reed frequencies shown. Most often the involved resonators are Helmholtz or quarter-wave, but mostly Helmholtz. Notice that as the reed frequency increases, there is a greater chance that the cavity will produce a Helmholtz frequency that is close to the reed frequency (in bold). In these cases, the air vibration induced by the Helmholtz resonator disrupts the air oscillations that are required in the tongue's self-induced vibration. Hence, these are areas where the reed is likely to choke. For the longer reeds, the frequencies are much larger than what a Helmholtz resonator can supply, unless you consider the frequencies of the higher partials. Since in some cases second and third partials can compete with the fundamental, there remain possibilities for choking even with these reeds. The phenomenon of choking is not new, but explanations vary. As far as I can tell, you simply assert that the cavity length is the culprit, without any physical explanation on why that could happen. In the light of the Helmholtz calculation, it's misleading to focus only on the length. You say that you change the length and it does away with choking. Why does that work? My explanation is that when you change the length you change the cavity volume, and thus you change the natural vibration frequency of the Helmholtz resonator, moving it away from its conflict to tongue vibration. It's very simple. Many times in technology development, people come up with intuitive ideas to explain what they observe. Then along comes a theory that explains things very well, and this theory is based on a much broader body of knowledge, adding confidence to the theory. I think this is the case here. Despite it's complexities, the free reed is still subject to Fluid Mechanics and Acoustics, not magic. As an acoustic source, it can couple to other acoustic sources, something that you cannot understand unless you invoke those valuable and proven physical principles. That's why theory is so strong, when it works. Especially very simple theories, like this one. Best wishes and stay well, Tom www.bluesbox.biz- 31 replies
-
Bellows pressure and musical pitch
ttonon replied to ttonon's topic in Instrument Construction & Repair
Hi Alex, I presume that after the tuning bench, you measure the pitch while the reed plays in the instrument, note the difference between when on the tuning bench, put the reed back on the bench and change its pitch accordingly. It's important to accurately use the same pressure during the bench measurement. In my experience, the reed always sounds lower in pitch than when on the bench. But perhaps some of the higher pitched reeds have the same pitch between bench and instrument. Do you concur? Thanks for the very valuable and interesting info on the minimum pressure for sounding. I never would've guessed that you could go as low as 0.1 inch wc.- 31 replies
-
Bellows pressure and musical pitch
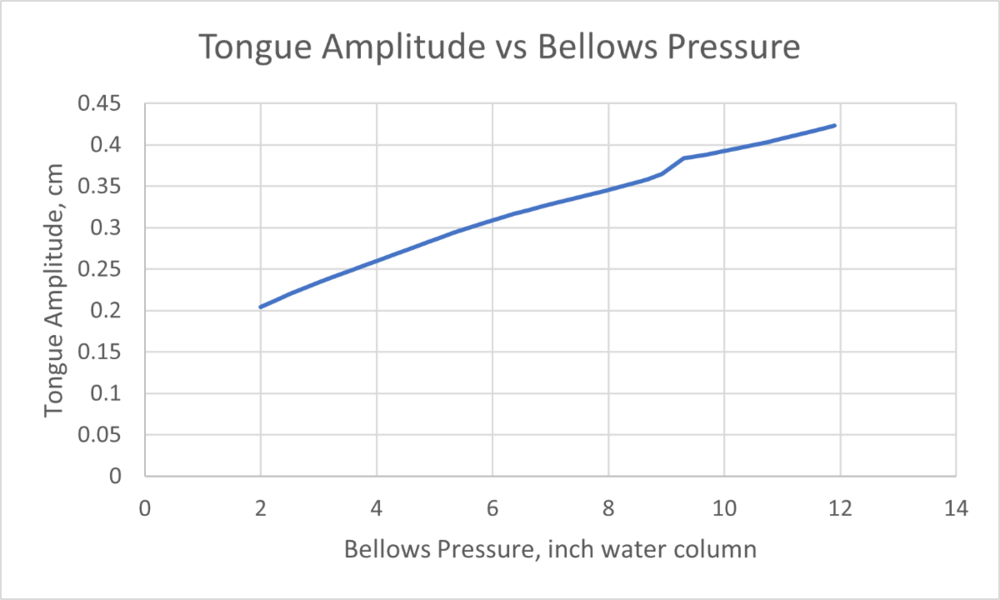
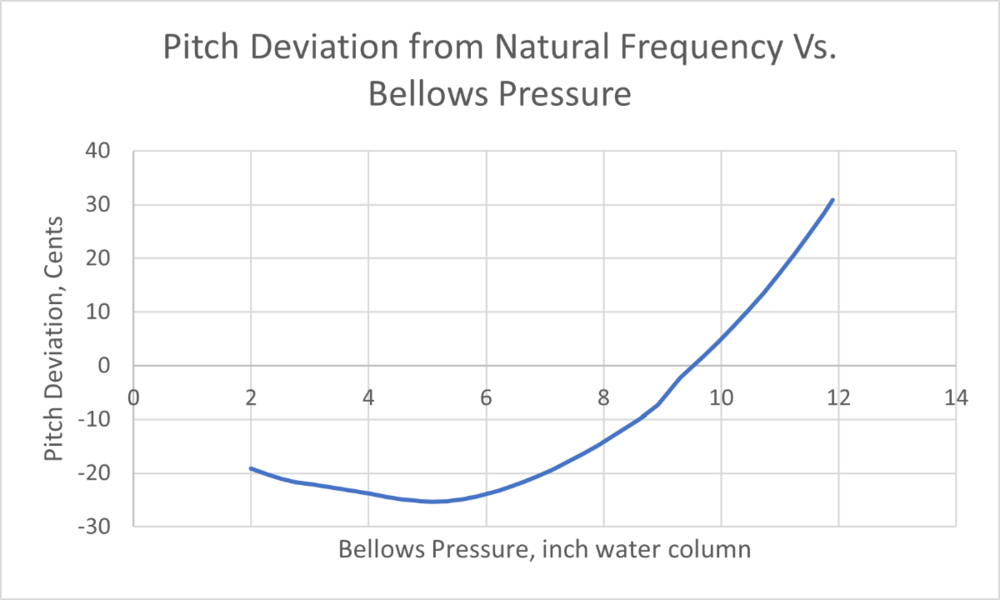
ttonon replied to ttonon's topic in Instrument Construction & Repair
Greetings to all, Thanks for the comments. I was hoping for more reports of detail - even quantitative measurements observed during tuning. Most of us have meters that can measure cents changes in musical notes, and perhaps some of the more curious have sometimes measured the bellows pressure during tuning. I understand that the needs of the maker are far more practical. But these other qualitative reports are also useful, and I'll glean from them as best I can. Many of you have mentioned the geometry of the cavity parameters, and that's also useful information. But let me explain here the fact that my present theoretical model, based on a fluid mechanical approach, does not include a cavity. This is only a first phase study, which basically takes the reed, mounts it in a wall that separates the static pressure on each side. The air blows through the reed and passes essentially into an infinite region with uniform pressure. Once I'm confident that the physical model for the basic tongue vibration works, I can then couple it to a resonator, or a cavity, using the appropriate physical principles. I'm under the impression (or hope) that not all cavity geometries affect very much the basic vibration of the reed tongue. (Some cavities have profound effect, as Dana describes.) This vibration is completely different than the acoustic sound field we hear coming from it as a source for that sound. The pressure oscillations, of the order of the bellows pressure difference are orders of magnitude larger than those of the acoustic sound far field. I think it's reasonable to suppose that some cavity geometries may not affect tongue vibration very much. For instance, comments here suggest that only certain geometric feature can have an effect, but only in the most extreme cases. Here, I'm interested in the less extreme cases, hoping that it describes the behavior of the isolated reed. Some of the reporting here is convoluted with the authors' intuitive explanations of why these geometries can produce what they hear. Some of these underlying explanations are pretty good, while others are erroneous, or at least misleading, missing some key physical mechanisms. For instance, no one mentioned the effects of the volume of the cavity, in addition to its length and the port opening. But the volume also plays a significant acoustic role, and together with the port, forms a Helmholtz resonator which can have significant influence on both tongue vibration and the sound field. Again, I say "can have," because it's not always the case, at least on tongue vibration. The cavity length itself has an important role at the very high frequencies, when it can form the sizes of quarter wave tubes. There are some very practical effects such as what Dana mentions, with the formation of jet-like behavior during draw, and these are very difficult to theoretically model. But I cannot get into a detailed discussion on cavity effects here, other than point readers to an article I wrote for the International Concertina Association, in their Proceedings (PICA) Dec 2, 2009, titled, "Reed Cavity Design and Resonance": https://concertina.org/2009/12/05/reed-cavity-design-and-resonance/?doing_wp_cron=1630012537.5247180461883544921875 Comments on the postings here: Lukasz, much of what you say agrees with my own experience, though for midrange and high range reeds, I'd not think you could bring down the pitch 5 cents from increased bellows pressure. I must explore this more. Can you please give me an idea of a quantitative measure of the pressure needed to "overblow" a reed? What pressure magnitudes do you regard as "normal" playing pressures? Dana, your comment that reeds around C6 and above can go sharp at the higher practical pressures is useful. Again, can you give me any quantitative pressure info? What would be "higher practical pressures?" In fact, I'd be very curious to know the experience of people here with the absolute minimum pressure it takes to start most reeds. I agree that quiescent standoff distance is most important, but let's say for optimum standoff and other geometry, what are those pressures, which probably varies with the extremes of reed pitch. Alex, I think you make a good point about weighted reed tongues. Such issues and many others are exceedingly difficult to theoretically analyze. For those interested, I present here a graph of a plot I made from this Phase I theory, showing vibration frequency variations in cents vs bellows pressure. These solutions are for the case when the tongue appears below the reed plate, and thus the lowest pressures are higher than the minimum starting pressures, when the tongue remains in the slot. We can deal with the latter case later. The reference frequency is the calculated frequency treating the tongue as a cantilever beam. This calculated frequency is a bit higher than the frequency that occurs in practice, because of the effects of air friction and inertia. Thus in the second graph, we'd need to lower the natural frequency line a few cents. The model does account for air friction, aerodynamic drag and air inertia. These results seem consistent with some of the reporting here. The increase in frequency at the higher bellows pressure may also be realistic. Again, thanks and more as of and when. Best regards, Tom www.bluesbox.biz- 31 replies
-
The pendulum has swung back an I'm resuming my theoretical interest in how free reeds work and it would help me to decide on a physical model if I knew how the musical pitch varies with bellows pressure, if at all. I ask this question mainly to the makers, but also to other enthusiasts who do their own tuning and tinkering in a serious way. But please report what you are sure of. If you're not sure, that's perhaps evidence that pitch variations are very small. Ideally, it would be nice to have quantitative data, such as cents pitch change with so much change in pressure, inches or cm in water column. But even naked ear observations can be helpful, if they can be stated with confidence. It would also help in the ideal case if you could supply the magnitude of the bellows pressure along with the pitch information. What minimum and maximum values for bellows pressure do you subject your reeds to? What range of bellows pressure do you expect in all playing situations? I've read that at the lowest pressures, pitch may first decrease with increasing pressure, then might increase with pressure at the highest pressure levels. Has anyone observed this? In the near future, I hope to do my own experiments on this topic, and afterwards, I'll present the results. I think that the pressure/pitch behavior is most fundamental to the free reed, and so reliable characterization in practice would be most appreciated. Best regards, Tom www.bluesbox.biz
- 31 replies
-
Compression vs. extension springs and tempering...
ttonon replied to RAc's topic in Instrument Construction & Repair
Ruediger, congrats for coming up with a workable solution. Good luck with it. Tom -
Well, I guess a little bit of humor isn't too far off topic, and catswhiskers, I was secretly hoping you'd do some experiments on those buttons. Tom
-
Of course, thank you for your concerns (chuckle). I'll nominate you as our entire Health and Safety Department. Tom
-
Well okay, though I do laugh. What isn't poisonous, Chlorine bleach? In fact there are uncountable organic oxidizers used for all kinds of things, even available over the counter at drug stores. A typical example is ethanoic acid used to get rid of fungus on toenails. So the term "poisonous" has such a broad meaning it's not very useful. Better would be "toxic," and in virtually all instances, the toxicity is the very reason people use these things. For instance, ethanoic acid is toxic to the fungus that attacks toe nails. So Alex, forgive me for my chuckle, but it seems we hear now a bit too much concern for ways to protect people from hurting themselves in this post-Trump environment, resulting in much redundancy, like being careful to tell people not to drink the ethanoic acid, even though you'd have to squeeze the tiny bottle into your mouth and get past the searing, painful discomfort. Does such redundancy work, I mean when there are so many natural defenses at play? I have doubts, no matter how much redundancy there is. I hope I'm not being redundundundundant 🙂 Tom
-
Hi Frank, interesting point, and I want to make sure what's going on here, in detail. I think the depth of folds and the number of folds are independent parameters. Correct? It also makes sense to me that a shallow fold will require more force to open than a wider fold, simply because the part of the fold that flexes assumes a greater part of the fold material, resulting in less of a "lever distance" available to the musician, who must then exert more force. In addition, since the force required to bend individual folds is in series with all the other forces associated with the other folds in the bellows, the total force is equal to only one of the forces. Thus the total force to pull the bellows is only about equal to the force required to open only one of the folds. This applies to the force required to close the bellows, if the equilibrium position of the bellows is in an open position. Is that about how you'd sum it up? Thanks. Tom www.bluesbox.biz
-
You might also try the new household bleaches formulated with hydrogen peroxide, which is also used in medicine. Better yet, buy H2O2 at the drug store, which I believe is stronger than the residential products. Another suggestion is Oxalic Acid, an organic acid that is often used to whiten materials, as an alternative to Chlorine bleach. I'm particularly cautious about Chlorine bleach because of it's tendency to combine with the ever-present hydrocarbons, resulting Chlorohydrocarbons compounds, many of which are proven carcinogens. So unless you're adequately protected, I'd shy away from Chlorine. So why do municipalities chlorinate public water systems? Exactly! Tom www.bluesbox.biz
-
Hi Chris, I think you're right. I went to the site of a bandoneon restorer at https://www.alma-bandoneon.de/en/ and asked him the question. His response is below. Sorry for getting us all off on a crazy tangent of mine. It seems bandoneon makers have some unique ways to treat the leather valves. On the effect of tongue offset, what he says checks with the practices in accordions and concertinas. Hi Tom, thank you very much for your interest in my work. Your question relates to a topic in restoration where musicians and restorers split into two camps and which is much discussed. Technically, you have to keep in mind that at the time the bandoneons were made, leather was the only suitable material .The leather was relatively thin and very flexible, so that it could give way quickly when the reed swung and just as quickly folded back when playing in the other direction or the reed came to rest. However, over the years, leather will dry out and curl up towards the skin side (which is what you observed). Attempts have often been made to prevent or remedy this by making slight cuts in the surface of the leather. It is normal for the lamellas to stick out slightly from the reedplate, but rolled up lamellas cause unpleasant background noises and detuning. In addition, they also lead to a deterioration in the sound response and higher air consumption. When you look inside a bandoneon, you can only see the leather lamellas, which are opposite the reeds that you play in opening direction. In tango, the bandoneon is mainly played pulling, so that these leathers bend outwards more often. The lamellas inside are mostly much more flat ; ) Modern lamellas are usually made from a combination of leather and a thin plastic sheet. The leather lies on the reed plate and ensures a warmer tone and the foil bends the leather back into its position. Valves made of full plastic, as often used in the accordion, are not very popular with the bandoneon. They amplify the upper sound frequencies and the sound is "falsified“. Choke of the reeds in severe staccato has a different cause and depends on how the reeds are bent (adjusted) towards the reed plates. The rule here is that the less the tongues are bent, the easier it is for them to respond. However, this also means that they no longer work at high air pressure. Conversely, tongues that are bent up very far still respond well at high pressure, but consume more air and are insensitive. Lot of the old school bandoneon players are very conservative and swear on the original, 90-110 years old leathers, even if they are not perfect any more. Whether new or old lamellas is a matter of taste. However, rolled up valves prevent the instrument from functioning properly. The perfect adjustment of the reeds, voicing and choose of the right leather lamellas and tuning is the most difficult part in my job. Kind regards, Christoph